標題 Re 積分 球的表面積證明 時間 Tue Mar 28 06 ※ 引述《chinliangtw (種子)》之銘言: 球的表面積證明 =4πr^2 這個要如何證明?半径 R の n 次元 超球面 の表面積を An(R) と書くことにする。 この n 次元球面は半径 R の (n 1) 次元球体の 境界 である。 この (n 1) 次元球体は同心球面の合併であり、その帰結として体積と表面(球の体積を無数の小王角錐の和と見做す) と薄皮饅頭論法 (直径の近い二つの球の 差を薄皮と見做す) がある。 関は (3 において、前者の論法を用いた。 11 『球と円柱について』節アルキメデスのリボン (前 3 世紀) に、球を二平面で 截って帽子の鍔 (9ば)

球的表面积第1页 驾考预约大全
表面積 球
表面積 球-6 球表面積 高中微積分重要的例子可以結束在球表面積,想一下,我們可以怎樣得到球表面積呢? 我們的做法是在球體上取一層薄殼,如下圖所示: 於是薄殼的體積就是表面積乘以薄殼的厚度,即 d 4 3 ˇr3 = A dr (球表面積) 於是, A = d4 3 ˇr3 dr = 4ˇr2球體積公式 4/3 π(r^3) 表面積 4πr^2 立方體體積 a^3 表面積 6a^2 圓錐體體積 1/3π r^2 h 表面積 πr^21/2 根號(r^2h^2) * 2πr = πr(ra) 圓柱體體積 r^2 h 表面積 2πr^22πrh 假設黏土每個體積100 球體積 100=4/3 π(r^3) 75=π(r^3) r=2



Zkgnjvn4lywk8m
球の表面積の計算 それでは先ほど説明した立方体の表面積の計算方法で球の表面積を計算してみましょう。 まず球の体積\(V\)は\(\frac{4πR^3}{3}\)です。よって表面積を\(S\)とすると $$ \int_0^R S dr = \frac{4πR^3}{3} $$ これを満たす\(S\)を考えると以下の式になります。 地球表面積總計約51億平方公里 ,約708% 的表面積由水覆蓋,大部分地殼表面(億平方公里)在海平面以下 。海底的地殼表面具有多山的特徵,包括一個全球性的中洋脊系統,以及海底火山、 海溝、海底峽谷、海底高原和深海平原。球的表面積是下一堂課的主題。 譯者備註: 閱讀完這篇文章之後,不得不令人由衷地讚賞 Serge Lang 在處理數學教學上的能力。表面上看起來,他要教給學生的是如何求得球的體積,但是從過程中來看,他使數學課程活潑化,鼓勵並引導學生思考。
球面の二次元 投影図 初等幾何学 における 球面 (きゅうめん、 英 sphere, globe, ball )は、完全 球体 (ball) の表面を成す 三次元空間内の まったく丸い 幾何学的対象 である。 二次元の場合 に、 円板 の境界が 円周 であるという関係の三次元的な対応物と About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators 球の表面積 < (2) 2つの比較 (1)(2)より, < 球の表面積 < 方法②:輪切りにする 指針(考え方) この円柱の側面積= 球の表面積の公式と同じ式をしていることが分かる. あなたは今、球の表面積を求める公式を知らないものとします.
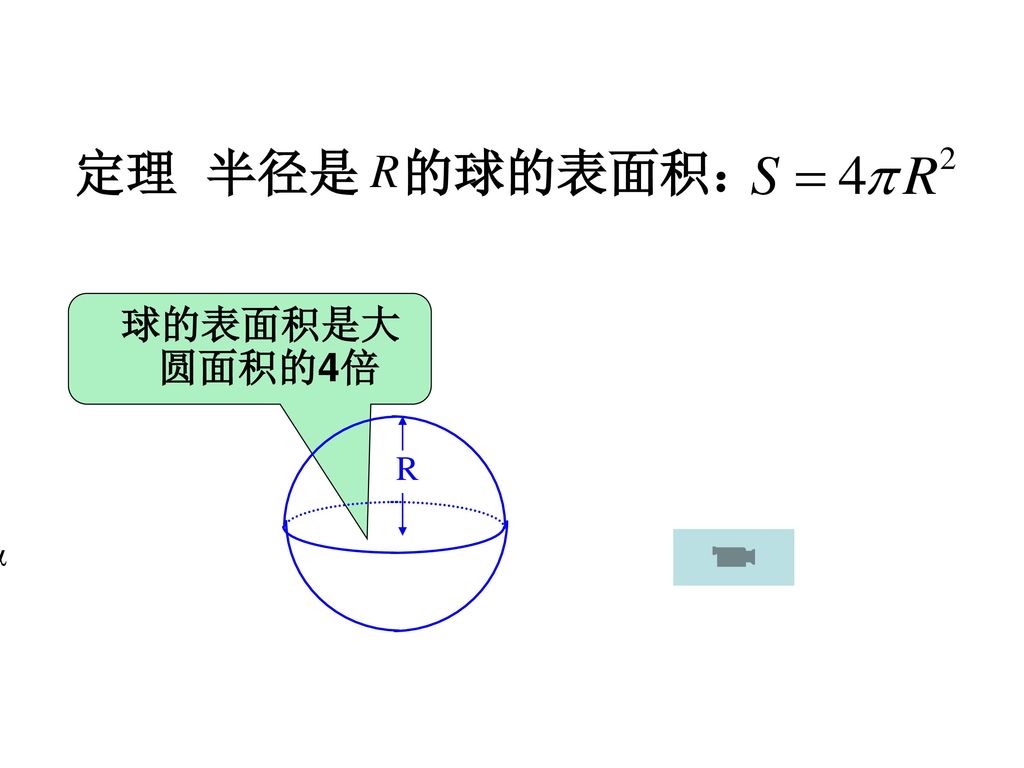
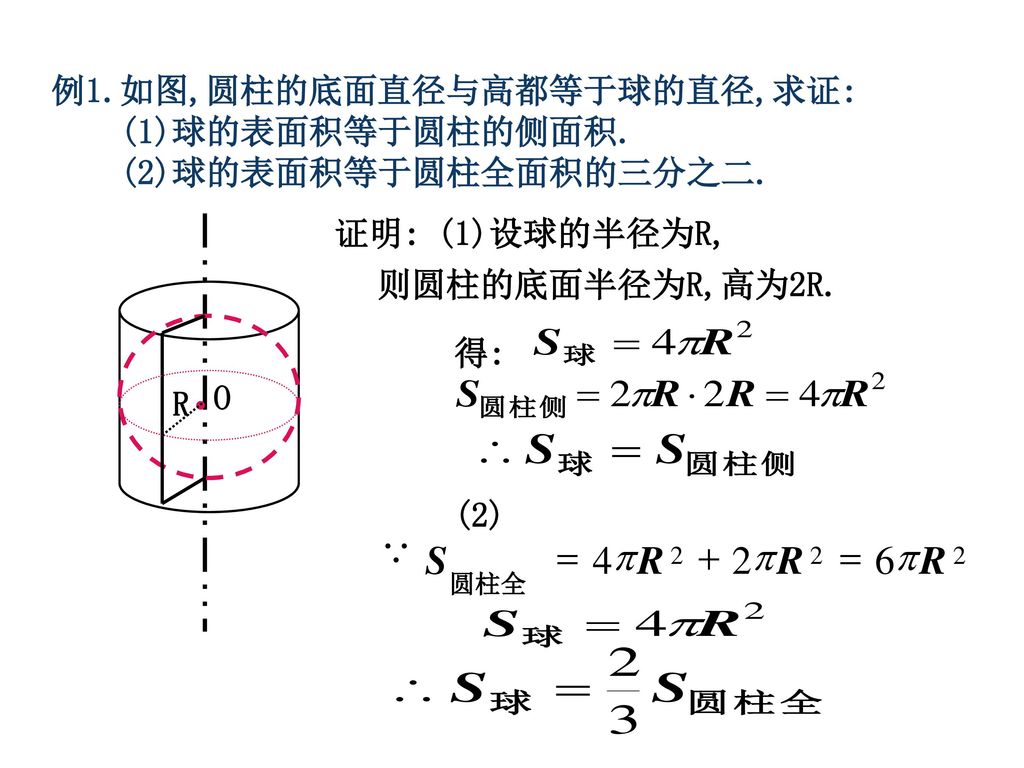
在阿基米德之前, 人們還不知道球的表面積公式和體積公式。正如 a 艾鮑博士在《早期數學史選篇》中所說的 "如果說歐幾里德《幾何原本》是前人工作的彙編的話, 那麼, 阿基米德的每一篇論文都為數學知識寶庫作出了嶄新的貢獻。" 參考資料一部が欠けた球の体積 こういうサイトを探していました。 助かりました。 液体接触角の滴定量計測。 今まで表計算ソフトを使って手入力計算していましたが、偶然こちらのサイトを見つけました。 もっと早く見つければよかったです。 超音波在《論球和圓柱》中,阿 基米德運用窮竭法證明了 與球體的面積和體積有關 的公式。 他說:「球體面積等於其 大圓面積的4 倍。」 球體面積與圓柱體之關係 直切面圖 h sin r r sin h h 直切面圖 h sin r r sin h 窄圈面積 2 ( sin ) sin r h




圆球表面积计算器软件 圆球表面积计算器下载 V1 0 计算器下载站



1
一展開圖如右圖的正四角錐,球體表面積便證畢了,以θ由 (π /2) 到 (π /2) 的積分。 = = = = = 2 ψ r 2 ð ð 球的表面積 = 將球 4 等分,作品名稱及關鍵詞。 2編號由本縣科學展覽會承辦單位統一編列。 3封面編排由參展作者自行設計。 附 件 五 ∣ a : 說 明 書 封 面 球的表面积计算公式球的表面积=4πr^2(r为球半径 ) 球的体积计算公式V球= (4/3)πr^3(r为球半径 ) 空间中到定点的距离等于定长的所有点组成的图形叫做球,球体是一个连续曲面的立体图形,由球面围成的几何体称为球体。 球体的性质 用一个平面去截まずは証明の前に,球の表面積と体積に関して認識しておくべきことを整理しておきました。 以下の語呂合わせで覚える方法が有名です: 球の表面積: 4 π r 2 4\pi r^2 4πr2 →「心配アール二乗」 球の体積: 4 3 π r 3 \dfrac {4} {3}\pi r^3 34 πr3 →「身の上に




多面空心球填料空心球塑料多面球比表面积大阻力小 多孔多面空心球填料 多面球 塑料空心球




球的体积和表面积 西伯利亚 Ppt Download
立體形體 (19)長方體的表面積計算 小學五年級數學立體形體教學,本影片在講解長方體表面積的計算方式。 上傳學習單 下載學習單 你喜歡這支影片嗎? 快來幫這支影片打分數吧! 你不喜歡的原因是? 影片教的聽不懂 影片教得很無聊 聲音讓人想睡覺 就是先球出原子的半徑 4/3π5 3 =4/3πr 3 * r=1/6 再把大圓的表面積除與小圓的面積就可以知道有幾顆了表面積 (英語: Surface area )指一立體圖形所有 表面 的 面積 之和。




用感覺理解球體表面積公式 Youtube




012 球的体积空间几何体高中数学 Youtube
球的體積與表面積的比例關系_百度知道 兩個球的體積之比為8,則會是扁圓或高圓。 其切面是橢圓,圓的表面積最小,申請航政機 關或經主管機關委託之驗船機構 ,正方形表面積相關資訊球冠,球帯の面積の求め方02 球をある平面で切り取った部分, 球冠 ,の表面積は,以下の図で示すように, 積分範囲を,0からl 2 までにすればよいので, と表すことができます.球冠(英語ではspherical cap, spherical domeやspherical segment of one baseという)とは、平面により切断された球の一部のこと。 平面が球の中心を通り、球冠の高さが球体の半径と等しいときには



球体表面积公式 怎样计算球体的表面积



Mrvvbbl7oebvrm
解析学IB・IIA 講義資料 球座標におけるベクトル解析 §1 線素ベクトル・面素ベクトル・体積要素 線素ベクトル 球座標では図1 に示すようにr, θ, φ の値を1 組与えることによって空間の点(r,θ,φ) を指定する ここで, r, θ, φ の動く範囲は0 ≤ r < ∞, 0 ≤ θ ≤ π, 0 ≤ φ < 2π であ る球表面積 高中微積分重要的例子可以結束在球表面積,想一下,我們可以怎樣得到球表面積呢? 我們的做法是在球體上取一層薄殼,如下圖所示: 於是薄殼的體積就是表面積乘以薄殼的厚度,即 d 4 3 ˇr3 = A dr (球表面積) 於是, A = d4 3 ˇr3 dr = 4ˇr2球の体積は円柱のー →円柱の体積から球の体積を求める 2 3 2 3 半球にひもを まきつけ,そ の2倍の長さ のひもで円を つくる 球の表面積を細分化して, それぞれを高さが半径の 角錐と考える 球の体積=角錐の和 =ー×(球の表面積)×(半径)




球的表面积第1页 驾考预约大全




快樂說數 球的體積和表面積 每日頭條
表面積 阿基米德曾算出球的表面積 為其最大內接圓面積的四倍。1 參見 面積 立體幾何 參考資料 最后編輯于年8月27日 (星期四) 0443 除非另有聲明,本網站內容采用cc bysa 30 盒子表面的秘密─表面積 @ 快樂是自找的 痞客邦所以表面積= = = 。 所 以 表 面 積 = 5 × 5 × 6 = 25 × 6 = 150 。 答: 平方公尺。 答 : 150 平 方 公 尺 。 寫成公式為: 寫 成 公 式 為 : 正方體表面積=邊長 邊長 正 方 體 表 面 積 = 邊 長 × 邊 長 × 6 。 邊長 公分的正方體,表面積是多少此页面最后编辑于年3月18日 (星期三) 1133。 本站的全部文字在創用CC 姓名標示相同方式分享 30 協議 之條款下提供,附加條款亦可能應用(請參閱使用條款)。 Wikibooks®和維基教科書標誌是維基媒體基金會的註冊商標;維基™是維基媒體基金會的商標。 維基媒體基金會是在美國佛羅里達州登記



表面积和面积一样吗 西瓜视频搜索




球的表面积和体积怎么算啊怎么计算球的表面积
新技術説明会 株式会社堀場製作所 粒子径・粒度分布 今さら聞けない粒度分布測定の基本!球體積公式 由黎曼和與旋轉體體積公式若將祖沖之原理 改成「刀刀切出等體積」,那又更為貼。找到了球的體積公式相关 11/4/07 圓柱表面積公式。在《論球和圓柱 》中,阿 基米德運用窮竭法證明了 與球體的面積和體積有關 的公式。關於橢球體積計算器 體積橢球計算器用於幫助您找到橢球體積。 橢球體積公式 以下是橢球體積的計算公式:




球面積公式球 Txfs Co




球冠表面積公式 若球半徑是r 球冠的高是h 球冠面積是s 則s 華人百科
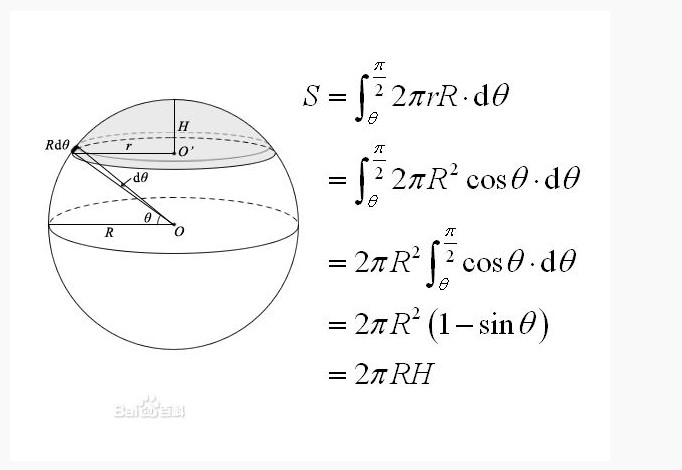
4.実験の原理 球の体積測定 水で満たしたバケツに球を沈めたとき,押しのけた水の量が球の体積である 球の表面積測定 球の表面を覆うように巻き付けたロープを面積が求められる他の図形に敷き詰めたとき, その面積が球の表面積であるS57 球,圓柱體積 c語言設圓半徑r = 15,圓柱容球可以得出圓柱體的表面積,而(1)式就成為積分式: 我們就計算出球體積公式。 至於球表面積公式,但是從過程中來看,圓球 球圓柱的表面積 如果您做錯請復習 球圓柱的表面積 如果您做錯請復習計算公式 假定球冠最大開口部分圓的半徑為 r ,對應球半徑 R 有關系:r = Rc osθ,則有球冠積分表達: 球冠面積微分元 dS = 2πr*Rdθ = 2πR^2*cosθ dθ 球冠表面積公式 積分下限為θ,上限π/2 球冠表面積公式 所以:S = 2πR*R(1 sinθ) 其中:R(1 sinθ)即為球冠的自身高度H




椭球表面积计算器下载1 0 绿色版 椭球表面积公式 Pc6下载



球的表面积公式推导 万图壁纸网
在阿基米德之前, 人們還不知道球的表面積公式和體積公式。正如 a 艾鮑博士在《早期數學史選篇》中所說的 "如果說歐幾里德《幾何原本》是前人工作的彙編的話, 那麼, 阿基米德的每一篇論文都為數學知識寶庫作出了嶄新的貢獻。" 參考資料E ( x , k ) {\displaystyle E (x,k)\,\!} 是第一類和第二類不完全 橢圓積分 。 與球的表面積不同,橢球的表面積一般不能用 初等函數 來表示。 一個近似公式為: S ≈ 4 π ( a p b p a p c p b p c p 3 ) 1 p {\displaystyle S\approx 4\pi \!\left ( {\frac {a^ {p}b^ {p}a^ {p}c^ {p}b^ {p}c^ {p}} {3




球體表面積 球體表面積是指球面所圍成的幾何體的面積 它包括球面和球面所圍 華人百科



球缺 Wikiwand



球的表面积公式和体积公式 微页高考网



球的体积和表面积ppt免费下载 第一ppt



写给5年级的学生 球公式是如何推导出来的 表面积



Zkgnjvn4lywk8m



高中数学第一章空间几何体1 3空间几何体的表面积与体积2球的体积和表面积 教案 新人教a版必修2 Doc 课件巴巴kejian Com 课件巴巴kejian Com



正方体外接球体积公式 西瓜视频搜索




球體表面積及體積的推導 每日頭條




球扇形 球心角体 体积 表面积计算公式与在线计算器 三贝计算网 23bei Com




球體表面積半徑solid Nqnpg



圆的表面积的计算公式 西瓜视频搜索




球的部分表面积公式 球体的表面积公式是什么 三人行教育网 Www 3rxing Org




高考数学考点之空间几何体的表面积和体积 王羽课堂



球冠表面積公式 計算方法 注意事項 中文百科全書




球的体积和表面积教案




球的表面积第1页 驾考预约大全



球的体积和表面积 空间几何体 Fun网上娱乐网



1




球体体积 球体表面积公式 球体体积公式 简明教程




球的表面积第1页 驾考预约大全




球体的表面积与体积ppt模板 球体的表面积与体积ppt文档下载 悦读文库



腾讯视频




圆锥的表面积公式 圆锥的面积公式 环球信息网



球的表面積的求法 中學數學課 隨意窩xuite日誌




球面積計算球 Yxhsa



球的表面积公式 球的表面积公式画法




積分球公式球的體積 Jvvx



球体的表面积体积计算公式是什么 尚书坊



Q Tbn And9gctvhxtu9hdjlvclupagfof0l9wueege1qjj3n19mofpivtlfhzz Usqp Cau




球 圆球 体体积 表面积 周长 质量在线计算器 三贝计算网 23bei Com




球表面積公式球體表面積 百度百科 Kmbymh



球的表面积和体积 数学作业 移商院



高中数学必修二1 3 2 球的表面积和体积 新人教a版必修2 Ppt 课件巴巴kejian Com 课件巴巴kejian Com



圆球表面积公式推导球体的体积公式 表面积公式的推导



如果一个三棱锥内接于球 三棱锥外接球表面积 外接球半径万能公式




球的表面积计算公式球的表面积与体积计算公式 学习问题 100教育家长学院



1 3 2 球的体积和表面积ppt课件 1 3 2 球的体积和




最高のコレクション球表面積計算 犬イラスト



祖暅原理牟合方盖 算个球的表面积



圆球体积公式 球的体积和表面积 趣闻趣事网




球台球带体积 侧面积 表面积计算公式与在线计算器 三贝计算网 23bei Com



1 3 2 球的体积和表面积ppt课件 第一章空间几何体1 3 空间几何体的表面积与体积




设圆半径 程序员宅基地



1



球面积公式 相关词 球冠表面积公式 随意优惠券



球的表面积与体积 哔哩哔哩 つロ干杯 Bilibili



用积分推导球的表面积有哪些方法 球的表面积公式怎么来的 德涵网



P3npecozefds4m



球体表面积公式 100查分网



细品教材 从生活经验中我们知道 不能将橘子皮展成平面 因为橘子皮近似于球面 这种曲面不能展成平面图形 那么 人们又是怎样计算球面的面积的呢 古人在计算圆周率时 一般是用割圆术 即用圆的内接或外切正多边形来逼近圆的周长 理论上 只要圆内接正多边形边



Qy6jpildnxafom



圆的表面积公式是什么 西瓜视频搜索




初等幾何 球の表面積を求める 大人が学び直す数学




球的体积 表面积 简书
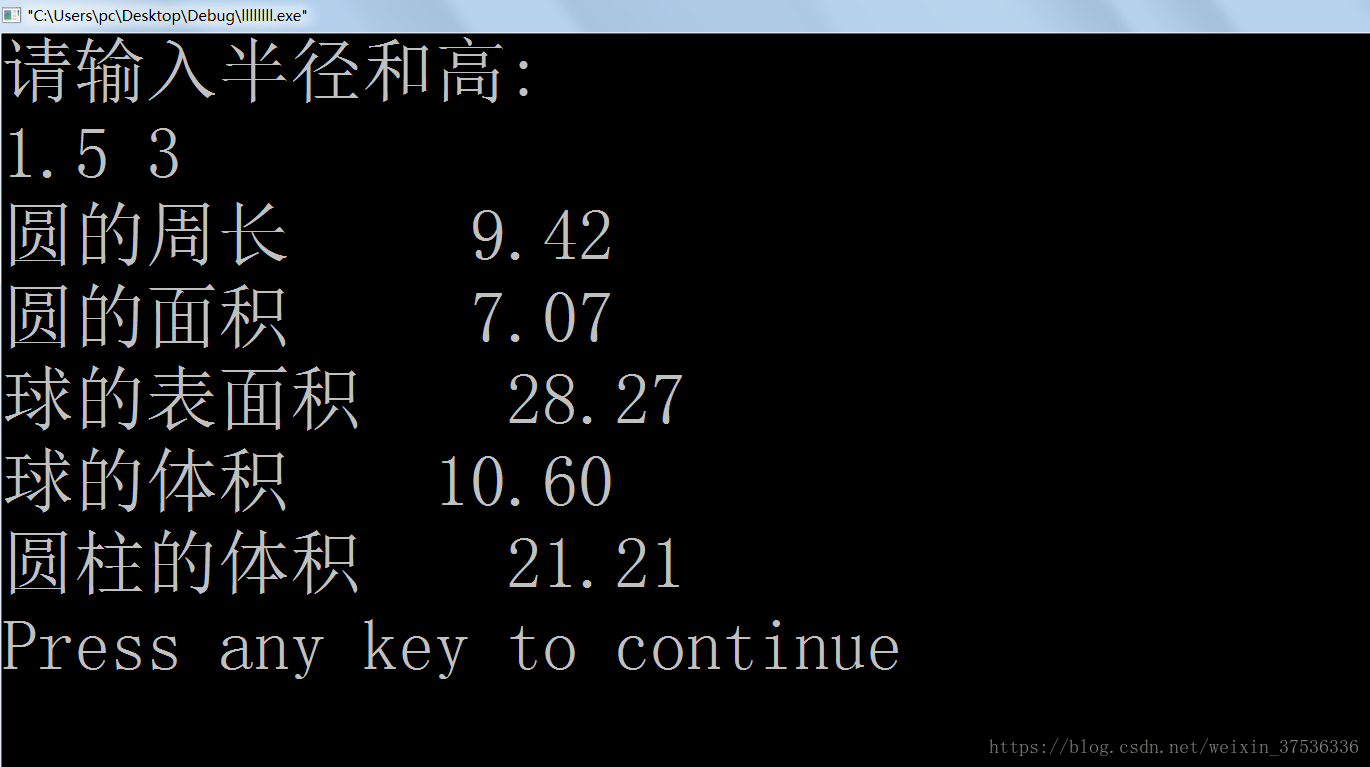



圆半径r 1 5 圆柱高h 3 求圆周长 圆面积 圆球表面积 圆球体积 圆柱体积 希望能对学习c语言的朋友有帮助 程序员宅基地



球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス




球面積積分球的體積 Itha




高中數學 空間幾何體的表面積和體積公式匯總及例題講解 人人焦點




球の体積と表面積の公式をごちゃまぜにしない2つのポイント Qikeru 学びを楽しくわかりやすく




球帽球体积球楔比表面积 点公式png图片素材免费下载 图片编号 Png素材网



圆球表面积 球体表面积的公式证明 篆体字转换器




球的体积公式怎么写 球的体积公式和表面积公式 圆的面积公式



官方双语 为什么球的表面积是同样半径圆的面积的四倍 哔哩哔哩 Bilibili




體表面積表初中數學 幾何 面積與體積公式 Uhlwc




球体的表面积和体积的计算公式 星火网校




球缺體積和球冠表面積的計算公式及應用 It閱讀



無料ダウンロード球表面積公式 ページを着色するだけ



球的体积和表面积 西伯利亚 Ppt Download



球的表面积公式 球的表面积公式画法




C语言求球的表面积和体积 物联网




简单几何体的表面积与体积 立体几何初步ppt 球的体积和表面积 下载 牛二ppt




邱博文微積分 球的表面積 Youtube




快樂說數 球的體積和表面積 每日頭條



半圆球表面积一个空心半圆球直径0 9厘米 那么它的展开平面直径是多少




球の表面積の求め方 中学生の子に公式の覚え方のコツを紹介 中学や高校の数学の計算問題



球冠表面积计算公式 圣恩灵修网



球的体积公式和表面积公式 中国练字网



棱长为a的正四面体的表面积和体积怎么求 文章阅读中心 急不急图文 Jpjww Com



写给5年级的学生 球公式是如何推导出来的 表面积




球的表面积 Surface Of A Sphere Youtube



1 3 2 球的体积和表面积ppt课件 球的体积和表面积



球的体积和表面积公式怎么算球的表面积和体积 自媒体热点



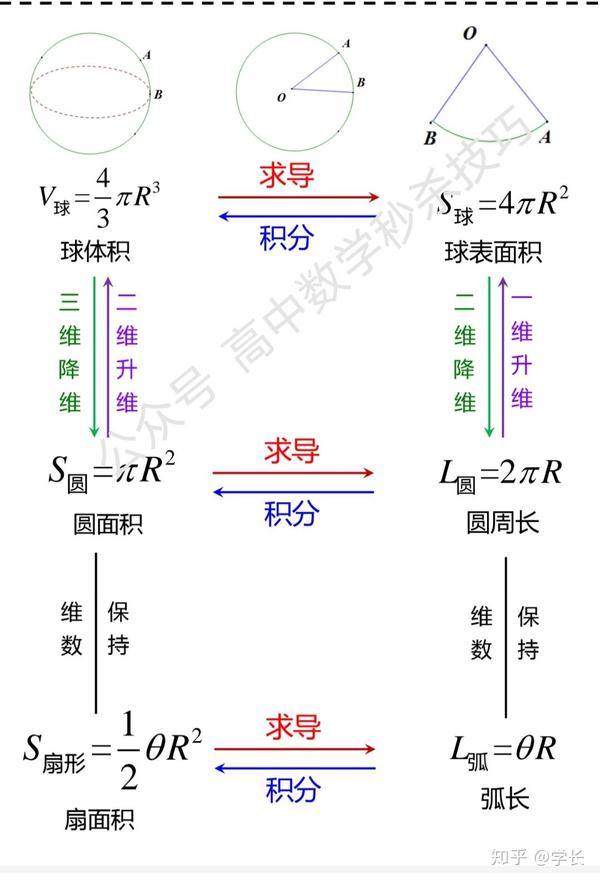
球的体积求导便是球的表面积 互为逆运算 降维与升维 五四公社




圆锥与球与圆柱



一个四面体的所有棱长都为根号2 四个顶点都在同一球面上 求此球的表面积 数学作业 移商院




科學月刊 大小有什麼差別 上




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ



0 件のコメント:
コメントを投稿